A number of non-contact techniques for metrology, ranging, and surface profiling have been developed over the years, including interferometry, moiré fringe topography, and time-of-flight (TOF) methods such as LIDAR. This type of technique is most valuable in the field of civil engineering, construction, surveying, and industrial plant maintenance, quality control, component identification, etc. Lasers have for many years provided a means for improved precision and accuracy in metrology applications. One commercially available method used today utilizes high-accuracy RF phase detection of a modulated laser beam reflected from a target. However, at the Japanese National Institute of Advanced Industrial Science and Technology (AIST) Metrology Institute, researchers have demonstrated an improved method which uses a femtosecond, mode-locked fiber laser (IMRA Femtolite C-15) to obtain unprecedented levels of accuracy over long distances.1 IMRA’s Femtolite 780 product line, which included the C-15, was the predecessor of IMRA’s current high performance series of miniature femtosecond fiber lasers. Performing measurements in the optical testing tunnel at AIST, an absolute accuracy of millimeters can be obtained for targets at a range of over 200 meters, with a position sensitivity of tens of microns.2
Principle of operation
When a sinusoidally modulated laser beam is reflected from a target at a range D, the returned beam has an RF-phase shift which is proportional to the distance to the target, according to
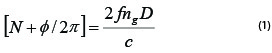
Here, N is the integer part of the phase, c is the speed of light, f is the modulation frequency used for measurement, and ng is the group refractive index at the optical wavelength. In this case, since a mode-locked pulse train is being used as the modulated source, a variety of modulation frequencies
![]()
are present which are all harmonics of the fundamental repetition frequency. In other words, a mode-locked pulse train is equivalent to a series of wide-ranging, modulated CW optical waves. Each of these modulated waves can be used in Equation 1.
We write the range D as
![]()
where D0 is an integral number of RF-wavelengths away from the target, as shown in Figure 1.
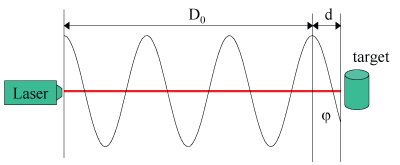
Figure 1: Schematic of a precision ranging system using a modulated laser beam.
This causes a cancellation in Equation 1, resulting in a fractional phase,
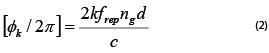
which can be measured to high precision (down to 0.1 degree) using an RF phase-meter.
In the ranging system shown in Figure 2, the IMRA Femtolite C-15 is used to provide a modelocked pulse train at two wavelengths, 1560 nm and its second harmonic at 780 nm. The fundamental repetition rate is frep ~ 50 MHz. At the 19th harmonic near f = 1 GHz, the beat note wavelength is 300 mm, and the fractional RF phase measurement accuracy of 0.1 degree gives an overall range sensitivity of approximately 50 microns, even at a target range of 240 meters.
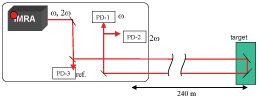
Figure 2: Schematic of a precision ranging system using a femtosecond modelocked fiber laser. Photodiodes PD-1 and PD-2 detect signals from the target at 1560 and 780 nm, respectively. PD-3 detects pulses directly from the laser as a reference.
This phase measurement at high modulation frequencies gives the highest precision. The cyclic error, resulting from ambiguity of the integer phase, can be eliminated by repeating the measurement using the lowest RF-frequency available, which is the 1st harmonic at frep = 50 MHz.
High-precision two-wavelength metrology technique
In addition to accurate measurement of the RF phase, a truly accurate distance measurement must account for variations in the group index of refraction of air, since this is an optical technique. That is to say, the measured optical distance is not the same as the absolute mechanical distance to the target unless the group index, ng , is known very precisely. It is well known that ng of air varies a function of temperature, pressure, and humidity, as well as wavelength according to the Edlén’s formulas. Using a two-wavelength measurement gives enough information to determine the mechanical distance to the target without the ambiguity of the refractive index of air.
In this method, the RF modulated distance measurement is repeated at both the 1560 nm and the 780 nm wavelengths. At each wavelength, the RF phase of the reflected beam is measured for the distant target at 240 meters, and also for nearby reference target at zero-distance. Through this comparison between the optical measurements and the Edlén’s formulas, based on the conditions of temperature, pressure and humidity, good agreement was found:
![]()
![]()
This demonstrates clearly that the group index of air can be measured accurately using the two-wavelength measurement.
With a precise measurement of the optical distance to the target and of the group refractive index of air, it is then possible to calculate the absolute mechanical distance to the target. In this experiment, it was found to be D = 239.943 ± 0.002 m, giving a fractional accuracy of 8 ppm. Table 1 summarizes the results obtained using the 20th harmonic near 1 GHz to measure the range to a target 240 meters distant.

Table 1: Measurement Accuracy
Higher precision in this type of application can be obtained by going to higher modulation frequencies (~ 10 GHz or higher), such that the RF wavelength of the modulation frequency is on the order of centimeters. This is easily achieved since the mode-locked pulse train contains modulation frequencies of 100’s of GHz, and even up to the THz range. Practically speaking, the upper usable frequency is limited by the bandwidth of the photodetector used in the measurement, and is typically in the range of 1 – 10 GHz.
Summary
By using the second harmonic as well as the fundamental output of mode-locked lasers to generate two optical wavelengths, it is now possible to perform high-precision ranging over hundreds of meters with accuracies of parts-per-million. This accuracy is obtained through a combination of precision RF phase measurement, frequency agility due to the large array of available modulation frequencies, and two-wavelength measurement of the group refractive index of air. This is made possible by the unique properties of mode-locked lasers. The very high sensitivity of this method will allow not only high-precision ranging, but also remote surface profiling of distant objects. Additionally, this method is closely related to frequency standards applications using the optical “comb” frequency generation which is being revolutionized by the ultrafast mode-locked laser field.
References
- K. Minoshimam, H. Matsumoto (2000). “High accuracy measurement of 240-m distance in an optical tunnel by use of a compact femtosecond laser,” Appl. Opt. Vol. 39, No. 30, pp. 5512-5517
- Measurement of 2 micrometers from 200 m distance using femtosecond optical comb: http://www.aist.go.jp/aist_e/aist_today/2003_09/hot_line/hot_line_24.html


